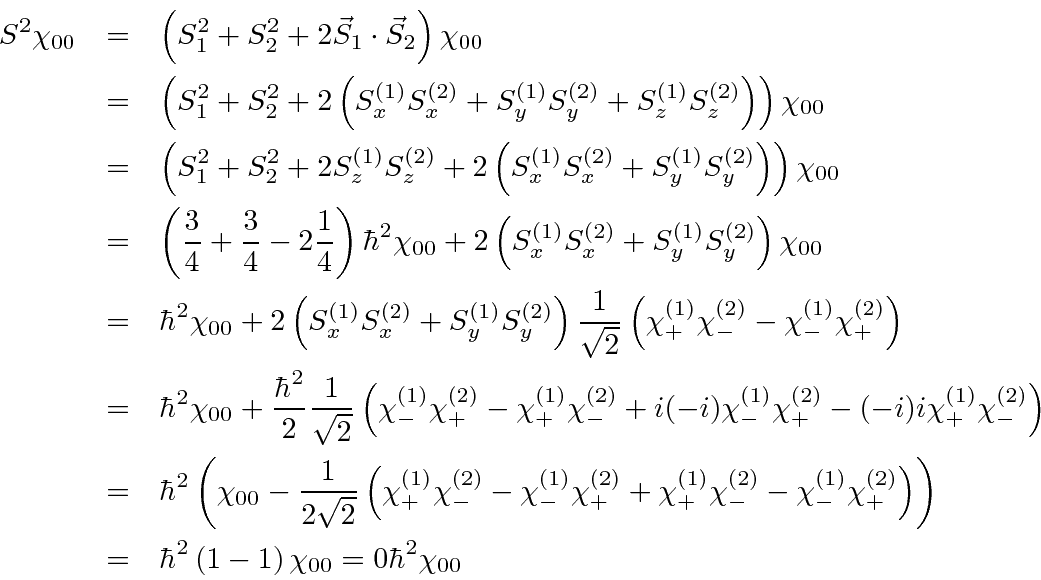Next: Adding any plus spin Up: Derivations and Computations Previous: Using the Lowering Operator Contents
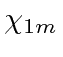 and
and
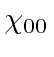 .
.
We wish to verify that the states we have deduced are really eigenstates of the
![]() operator.
We will really compute this in the most brute force.
operator.
We will really compute this in the most brute force.
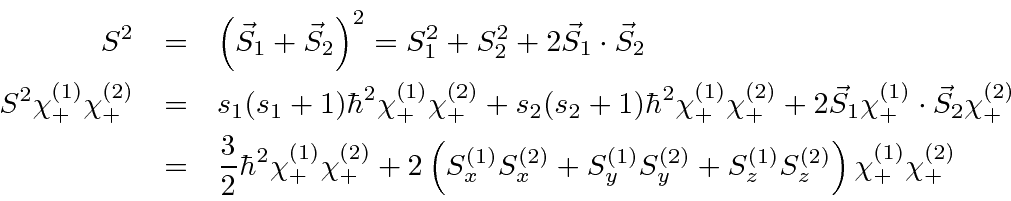
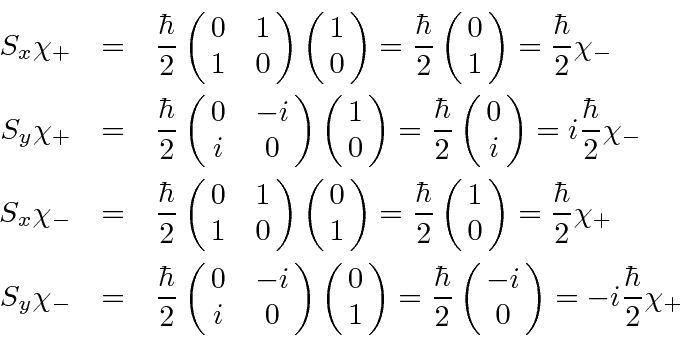
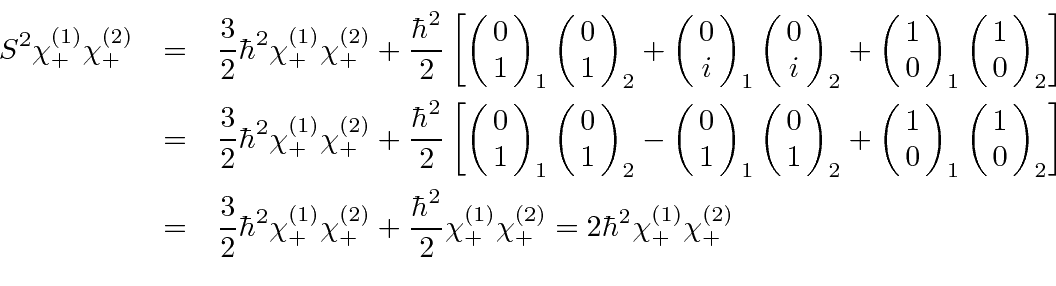
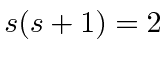 , so that the
, so that the
Now lets do the
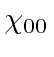 state.
state.