Next: Time Independent Perturbation Theory Up: Course Summary Previous: Local Phase Symmetry in Contents
It is often required to add angular momentum from two (or more) sources together to get states of definite total angular momentum. For example, in the absence of external fields, the energy eigenstates of Hydrogen (including all the fine structure effects) are also eigenstates of total angular momentum. This almost has to be true if there is spherical symmetry to the problem.
As an example, lets assume we are adding the orbital angular momentum from two electrons,
![]() and
and
![]() to get a total angular momentum
to get a total angular momentum
![]() .
We will show that the total angular momentum quantum number takes on every value in the range
.
We will show that the total angular momentum quantum number takes on every value in the range
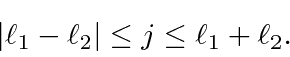
The states of definite total angular momentum with quantum numbers
![]() and
and
![]() ,
can be written in terms of products of the individual states
(like electron 1 is in this state AND electron 2 is in that state).
The general expansion is called the Clebsch-Gordan series:
,
can be written in terms of products of the individual states
(like electron 1 is in this state AND electron 2 is in that state).
The general expansion is called the Clebsch-Gordan series:
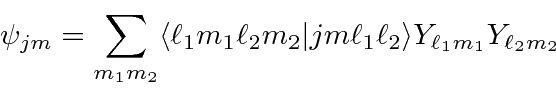
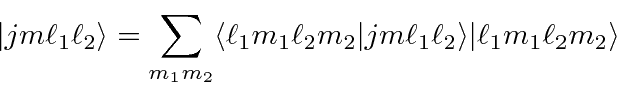
When combining states of identical particles,
the highest total angular momentum state,
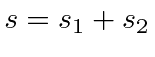 , will always be
symmetric under interchange.The symmetry under interchange will alternate as
, will always be
symmetric under interchange.The symmetry under interchange will alternate as
![]() is reduced.
is reduced.
The total number of states is always preserved.
For example if I add two
![]() states together, I get total angular
momentum states with
states together, I get total angular
momentum states with
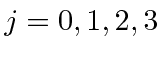 and 4.
There are 25 product states since each
and 4.
There are 25 product states since each
![]() state has 5 different possible
state has 5 different possible
![]() s.
Check that against the sum of the number of states we have just listed.
s.
Check that against the sum of the number of states we have just listed.
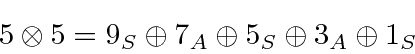
We will use addition of angular momentum to:
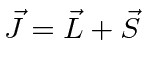 ;
;
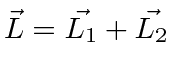 ;
;
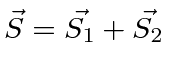 ;
;
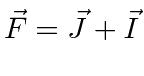 ;
;
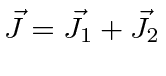 ;
;
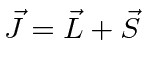 ;
;
Jim Branson 2013-04-22