Next: Energy States of Electrons Up: Derivations and Computations Previous: The Size of the Contents
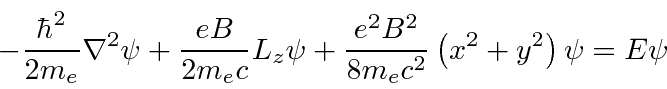
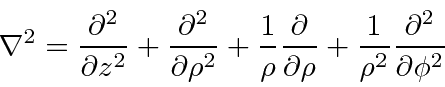
![\bgroup\color{black}$[H,p_z]=[H,L_z]=0$\egroup](img2699.png) .
These variables will be constants of the motion and we therefore choose
.
These variables will be constants of the motion and we therefore choose
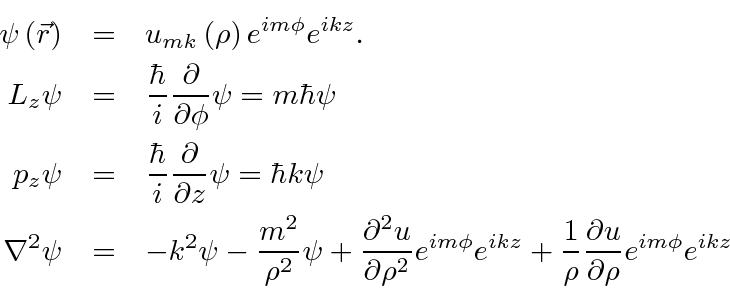
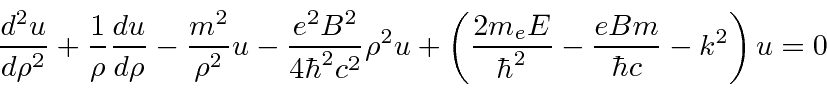
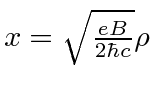 (dummy variable, not the coordinate) and
(dummy variable, not the coordinate) and
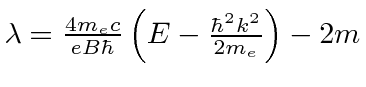 .
Then
.
Then
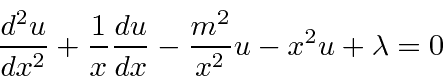
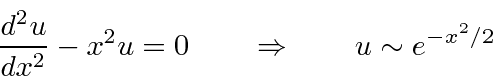
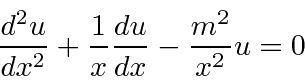
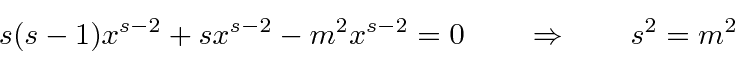
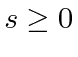
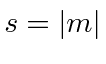
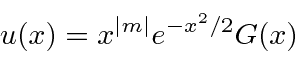
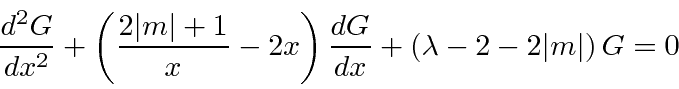
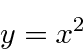
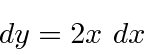
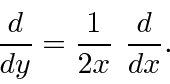
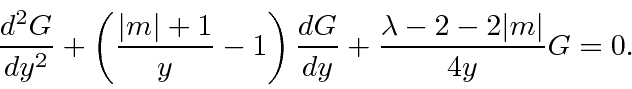
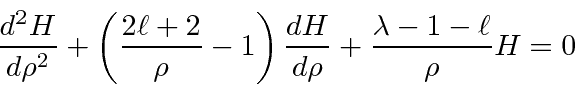
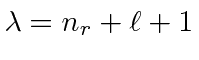 .
The equations are the same if WE set our
.
The equations are the same if WE set our
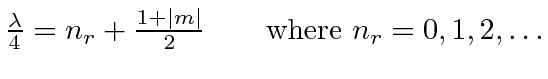 .
Recall that our
.
Recall that our
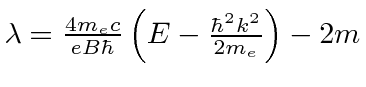 .
This gives us the energy eigenvalues
.
This gives us the energy eigenvalues
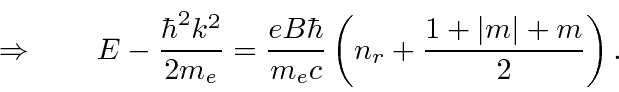
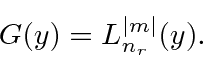
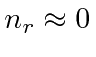 .
This is the classical limit.
.
This is the classical limit.
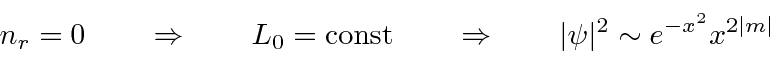
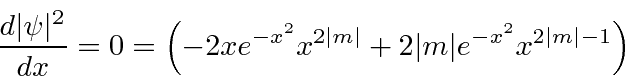
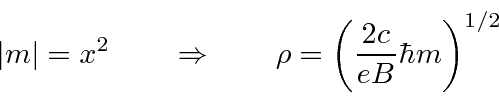
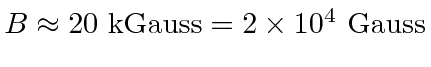 . Then
. Then
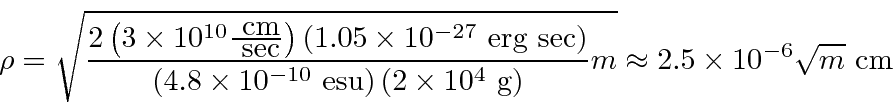
This can be compared to the purely classical calculation for an electron with
angular momentum
![]() which gives
which gives
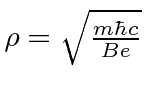 .
This simple calculation neglects to count the angular momentum stored in the field.
.
This simple calculation neglects to count the angular momentum stored in the field.
Jim Branson 2013-04-22