- *
We have shown that the Hermitian conjugate of a rotation operator
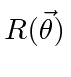 is
is
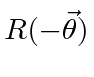 .
Use this to prove that if the
.
Use this to prove that if the 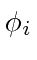 form an orthonormal complete set, then
the set
form an orthonormal complete set, then
the set
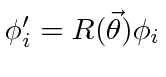 are also orthonormal and complete.
are also orthonormal and complete.
- Given that
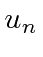 is the
is the 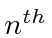 one dimensional harmonic oscillator energy eigenstate:
a) Evaluate the matrix element
one dimensional harmonic oscillator energy eigenstate:
a) Evaluate the matrix element
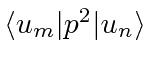 .
b) Write the upper left 5 by 5 part of the
.
b) Write the upper left 5 by 5 part of the 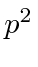 matrix.
matrix.
- A spin 1 system is in the following state in the usual
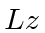 basis:
basis:
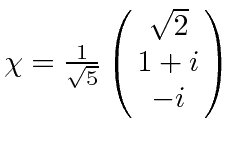 .
What is the probability that a measurement of the
.
What is the probability that a measurement of the 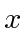 component of spin yields
zero?
What is the probability that a measurement of the
component of spin yields
zero?
What is the probability that a measurement of the 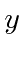 component of spin
yields
component of spin
yields 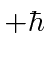 ?
?
- In a three state system, the matrix elements are given as
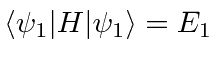 ,
,
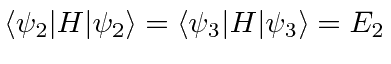 ,
,
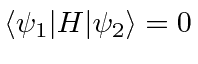 ,
,
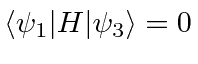 ,
and
,
and
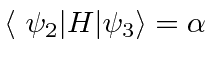 .
Assume all of the matrix elements are
real. What are the energy eigenvalues and eigenstates of the system?
At
.
Assume all of the matrix elements are
real. What are the energy eigenvalues and eigenstates of the system?
At 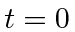 the system is in the state
the system is in the state 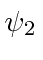 .
What is
.
What is 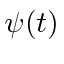 ?
?
- Find the (normalized) eigenvectors and eigenvalues of the
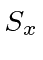 (matrix) operator for
(matrix) operator for 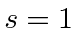 in the usual (
in the usual (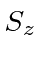 ) basis.
) basis.
- *
A spin
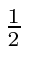 particle is in a magnetic field in the
particle is in a magnetic field in the 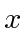 direction
giving a Hamiltonian
direction
giving a Hamiltonian
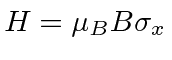 .
Find the time development (matrix) operator
.
Find the time development (matrix) operator
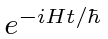 in the usual basis.
If
in the usual basis.
If
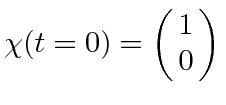 , find
, find 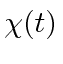 .
.
- A spin
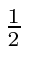 system is in the following state
in the usual
system is in the following state
in the usual 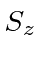 basis:
basis:
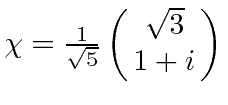 .
What is the probability that a measurement of the
.
What is the probability that a measurement of the 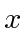 component of spin yields
component of spin yields
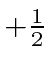 ?
?
- A spin
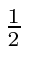 system is in the state
system is in the state
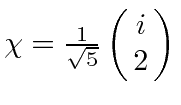 (in the usual
(in the usual 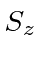 eigenstate basis).
What is the probability that a measurement of
eigenstate basis).
What is the probability that a measurement of 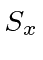 yields
yields
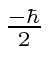 ?
What is the probability that a measurement of
?
What is the probability that a measurement of 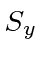 yields
yields
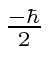 ?
?
- A spin
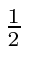 object is in an eigenstate of
object is in an eigenstate of 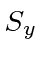 with eigenvalue
with eigenvalue 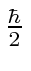 at t=0. The particle is in a magnetic
field
at t=0. The particle is in a magnetic
field 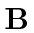 =
= 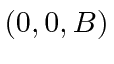 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
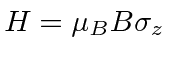 . Find the probability to measure
. Find the probability to measure
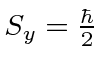 as a function of time.
as a function of time.
- Two degenerate eigenfunctions of the Hamiltonian are properly
normalized and have the following properties.
What are the properly normalized states that are eigenfunctions
of H and P?
What are their energies?
- What are the eigenvectors and eigenvalues for the spin
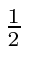 operator
operator 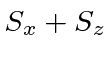 ?
?
- A spin
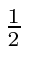 object is in an eigenstate of
object is in an eigenstate of 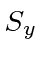 with eigenvalue
with eigenvalue 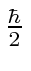 at t=0. The particle is in a magnetic
field
at t=0. The particle is in a magnetic
field 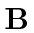 =
= 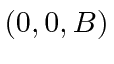 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
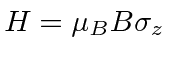 . Find the probability to measure
. Find the probability to measure
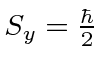 as a function of time.
as a function of time.
- A spin 1 system is in the following state, (in the usual
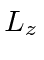 eigenstate basis):
eigenstate basis):
What is the probability that a measurement of 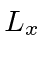 yields 0?
What is the probability that a measurement of
yields 0?
What is the probability that a measurement of 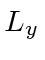 yields
yields 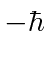 ?
?
- A spin
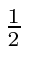 object is in an eigenstate of
object is in an eigenstate of 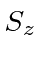 with eigenvalue
with eigenvalue 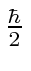 at t=0. The particle is in a magnetic
field
at t=0. The particle is in a magnetic
field 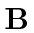 =
= 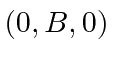 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
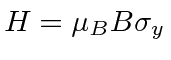 . Find the probability to measure
. Find the probability to measure
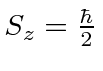 as a function of time.
as a function of time.
- A spin 1 particle is placed in an external field in the
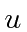 direction
such that the Hamiltonian is given by
direction
such that the Hamiltonian is given by
Find the energy eigenstates and eigenvalues.
- A (spin
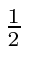 ) electron is in an eigenstate of
) electron is in an eigenstate of 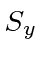 with eigenvalue
with eigenvalue
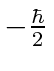 at
at 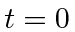 . The particle is in a magnetic
field
. The particle is in a magnetic
field 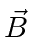 =
= 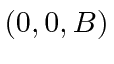 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
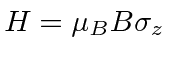 .
Find the spin state of the particle as a function of time.
Find the probability to measure
.
Find the spin state of the particle as a function of time.
Find the probability to measure
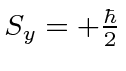 as a function of time.
as a function of time.
Jim Branson
2013-04-22
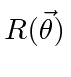 is
is
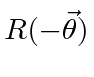 .
Use this to prove that if the
.
Use this to prove that if the 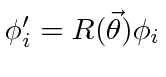 are also orthonormal and complete.
are also orthonormal and complete.
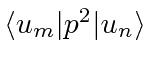 .
b) Write the upper left 5 by 5 part of the
.
b) Write the upper left 5 by 5 part of the 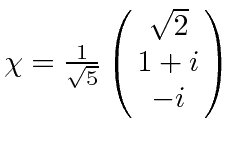 .
What is the probability that a measurement of the
.
What is the probability that a measurement of the  ?
?
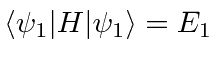 ,
,
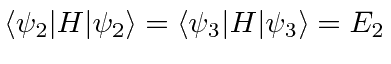 ,
,
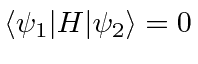 ,
,
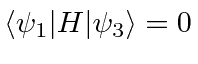 ,
and
,
and
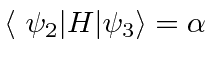 .
Assume all of the matrix elements are
real. What are the energy eigenvalues and eigenstates of the system?
At
.
Assume all of the matrix elements are
real. What are the energy eigenvalues and eigenstates of the system?
At 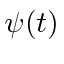 ?
?
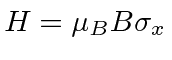 .
Find the time development (matrix) operator
.
Find the time development (matrix) operator
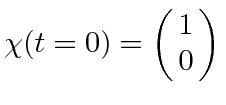 , find
, find 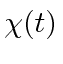 .
.
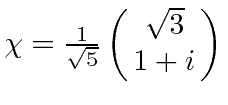 .
What is the probability that a measurement of the
.
What is the probability that a measurement of the 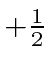 ?
?
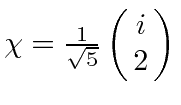 (in the usual
(in the usual 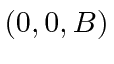 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
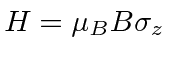 . Find the probability to measure
. Find the probability to measure
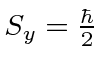 as a function of time.
as a function of time.
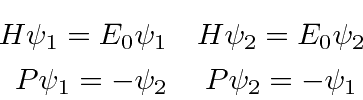
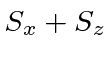 ?
?
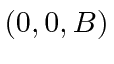 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
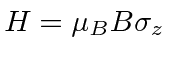 . Find the probability to measure
. Find the probability to measure
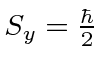 as a function of time.
as a function of time.
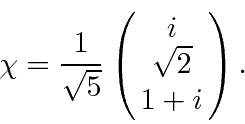
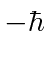 ?
?
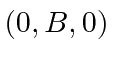 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
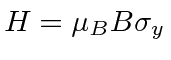 . Find the probability to measure
. Find the probability to measure
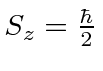 as a function of time.
as a function of time.
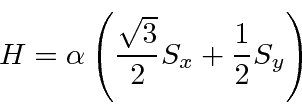
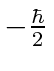 at
at 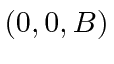 which makes the Hamiltonian for the system
which makes the Hamiltonian for the system
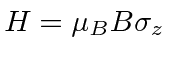 .
Find the spin state of the particle as a function of time.
Find the probability to measure
.
Find the spin state of the particle as a function of time.
Find the probability to measure
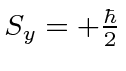 as a function of time.
as a function of time.