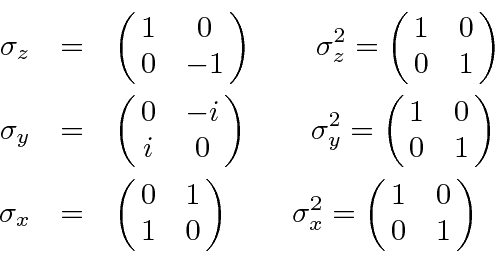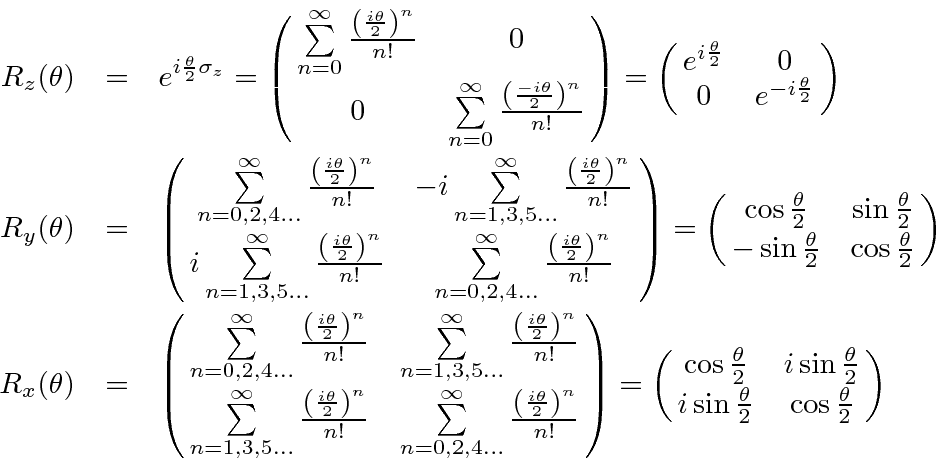Derive Spin
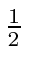 Rotation Matrices *
Rotation Matrices *
In section 18.11.3, we derived the expression for the rotation operator for
orbital angular momentum vectors.
The rotation operators for internal angular momentum will follow the same formula.
We now can compute the series by looking at the behavior of
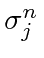 .
.
Doing the sums
Note that all of these rotation matrices become the identity matrix for rotations through 720 degrees
and are minus the identity for rotations through 360 degrees.
Jim Branson
2013-04-22
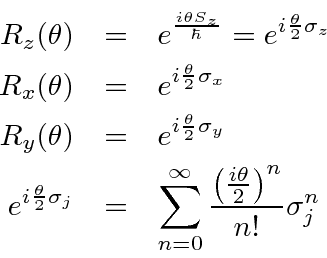
![]() .
.