Next: Compute the Rotation Operator Up: Derivations and Computations Previous: Derive the Expression for Contents
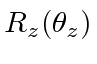 *
*
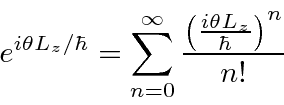
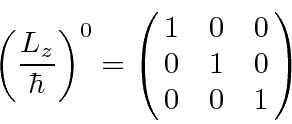
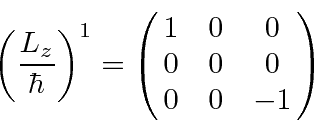
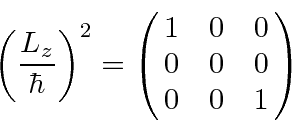
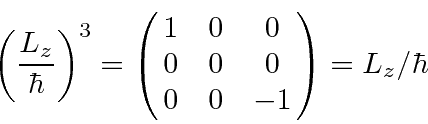
All the odd powers are the same. All the nonzero even powers are the same.
The
![]() s all cancel out.
We now must look at the sums for each term in the matrix and identify the function it
represents.
If we look at the sum for the upper left term of the matrix, we get a 1 times
s all cancel out.
We now must look at the sums for each term in the matrix and identify the function it
represents.
If we look at the sum for the upper left term of the matrix, we get a 1 times
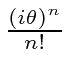 . This is just
. This is just
![]() .
There is only one contribution to the middle term, that is a one from
.
There is only one contribution to the middle term, that is a one from
![]() .
The lower right term is like the upper left except the odd terms have a
minus sign.
We get
.
The lower right term is like the upper left except the odd terms have a
minus sign.
We get
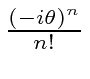 term n. This is just
term n. This is just
![]() .
The rest of the terms are zero.
.
The rest of the terms are zero.
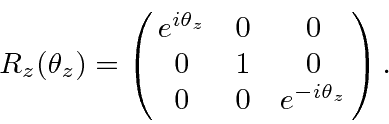
Jim Branson 2013-04-22