Next: Nuclear Magnetic Resonance (NMR Up: Examples Previous: Eigenvectors of Contents
Assume that we are in an arbitrary spin state
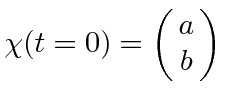 and we
have chosen the z axis to be in the field direction.
The upper component of the vector (a) is the amplitude to have spin up along the z direction,
and the lower component (b) is the amplitude to have spin down.
Because of our choice of axes, the spin up and spin down states are also the energy eigenstates
with energy eigenvalues of
and we
have chosen the z axis to be in the field direction.
The upper component of the vector (a) is the amplitude to have spin up along the z direction,
and the lower component (b) is the amplitude to have spin down.
Because of our choice of axes, the spin up and spin down states are also the energy eigenstates
with energy eigenvalues of
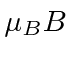 and
and
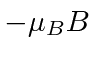 respectively.
We know that the energy eigenstates evolve with time quite simply (recall the separation of the
Schrödinger equation where
respectively.
We know that the energy eigenstates evolve with time quite simply (recall the separation of the
Schrödinger equation where
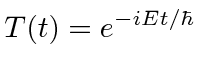 ).
So its simple to write down the time evolved state vector.
).
So its simple to write down the time evolved state vector.
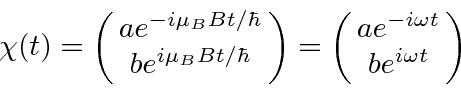
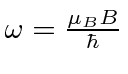 .
.
So let's say we start out in the state with spin up along the x axis,
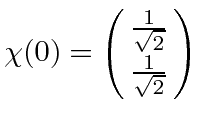 .
We then have
.
We then have
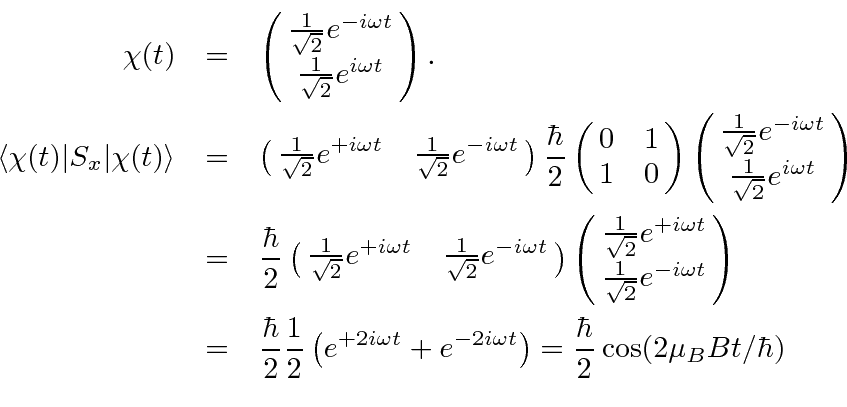
So again the spin precesses around the magnetic field. Because
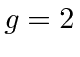 the rate is twice as
high as for
the rate is twice as
high as for
![]() .
.
Jim Branson 2013-04-22