Splitting the Eigenstates with Stern-Gerlach

A beam of atoms can be split into the eigenstates of $L_z$ with a Stern-Gerlach apparatus. A magnetic moment is associated with angular momentum.

$$\bgroup\color{black} \vec{\mu}={-e\over 2mc}\vec{L}=\mu_B{\vec{L}\over\hbar} \egroup$$

This magnetic moment interacts with an external field, adding a term to the Hamiltonian.

$$\bgroup\color{black} H=-\vec{\mu}\cdot\vec{B} \egroup$$

If the magnetic field has a gradient in the z direction, there is a force exerted (classically).

$$\bgroup\color{black} F=-{\partial U\over\partial z}=\mu_z{\partial B\over\partial z} \egroup$$

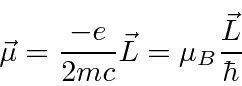
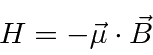
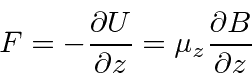
A magnet with a strong gradient to the field is shown below.

Lets assume the field gradient is in the z direction.

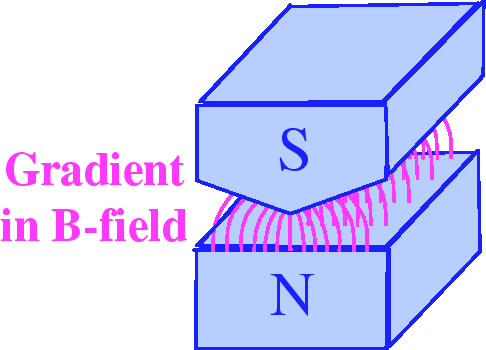
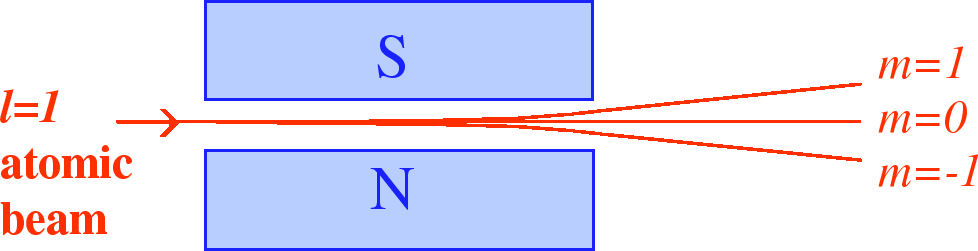
In the Stern-Gerlach experiment, a beam of atoms (assume $\ell=1$) is sent into a magnet with a strong field gradient. The atoms come from an oven through some collimator to form a beam. The beam is said to be unpolarized since the three m states are equally likely no particular state has been prepared. An unpolarized, $\ell=1$ beam of atoms will be split into the three beams (of equal intensity) corresponding to the different eigenvalues of $L_z$.

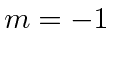The atoms in the top beam are in the $m=1$ state. If we put them through another Stern-Gerlach apparatus, they will all go into the top beam again. Similarly for the middle beam in the $m=0$ state and the lower beam in the $m=-1$ state.

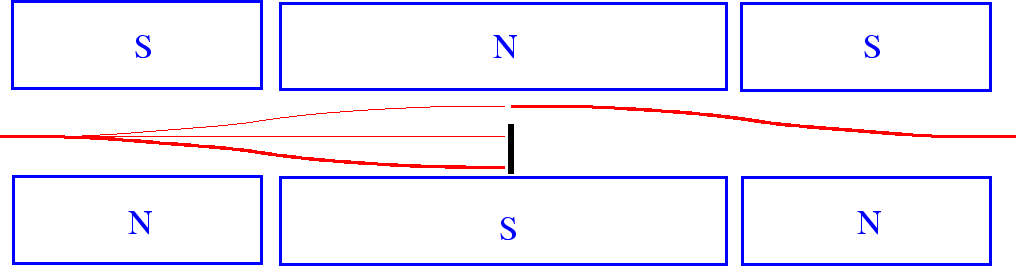
We can make a fancy Stern-Gerlach apparatus which puts the beam back together as shown below.

$\left\{\matrix{+ \cr 0 \cr - }\right\}_z\rightarrow$

We can represent the apparatus by the symbol to the right.

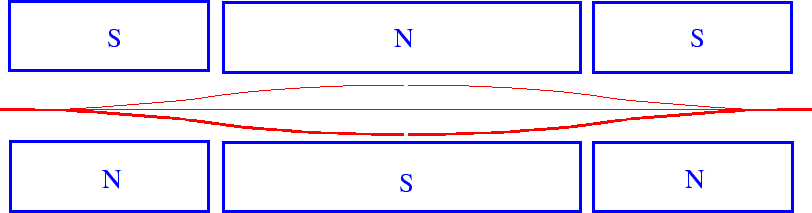
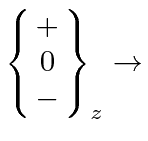
We can use this apparatus to prepare an eigenstate. The apparatus below picks out the $m=1$ state

$\left\{\matrix{+ \cr 0 \vert \cr - \vert}\right\}_z\rightarrow$

again representing the apparatus by the symbol at the right. We could also represent our apparatus plus blocking by an operator

$$\bgroup\color{black} O=\vert+\rangle\;\langle +\vert \egroup$$

where we are writing the states according to the $m$ value, either +, -, or 0. This is a projection operator onto the + state.

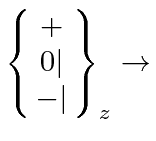
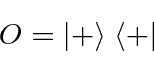
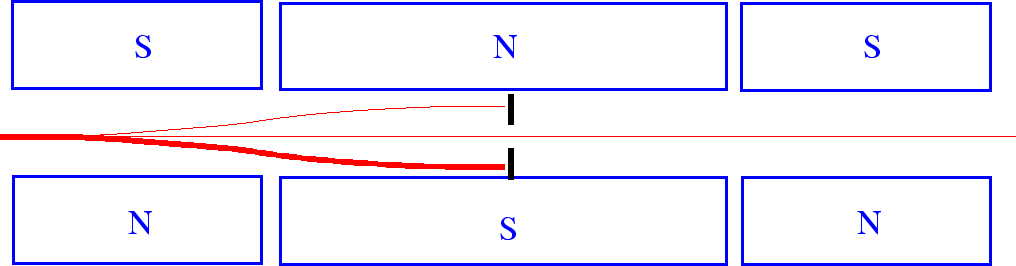
An apparatus which blocks both the + and - beams

$\left\{\matrix{+ \vert \cr 0 \cr - \vert}\right\}_z\rightarrow$

would be represented by the projection operator

$$\bgroup\color{black} O=\vert\rangle\;\langle 0\vert \egroup$$

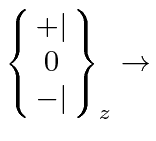
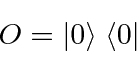
Similarly, an apparatus with no blocking could be written as the sum of the three projection operators.

$$\bgroup\color{black} \left\{\matrix{+ \cr 0 \cr - }\right\}_z... ...imits_{m=-1}^{+1} \vert z_m\rangle\;\langle z_m\vert =1 \egroup$$

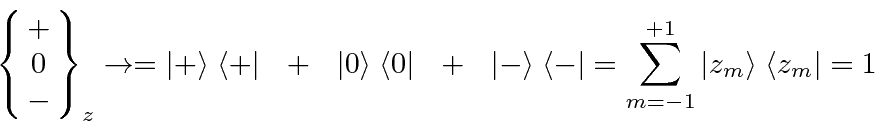
If we block only the $m=1$ beam, the apparatus would be represented by

$$\bgroup\color{black} \left\{\matrix{+ \vert \cr 0 \cr - }\rig... ...\;\langle 0\vert + \vert-\rangle\;\langle -\vert .\egroup$$

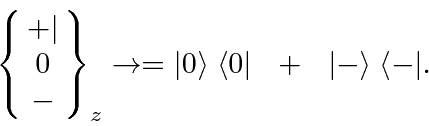
* Example: A series of Stern-Gerlachs.*