Next: The Expectation of in Up: Examples Previous: Examples Contents
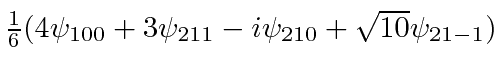 .
Find the expected value of the Energy,
.
Find the expected value of the Energy,
First check the normalization.
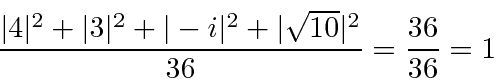
The terms are eigenstates of
![]() ,
,
![]() , and
, and
![]() , so we can easily compute expectation values
of those operators.
, so we can easily compute expectation values
of those operators.
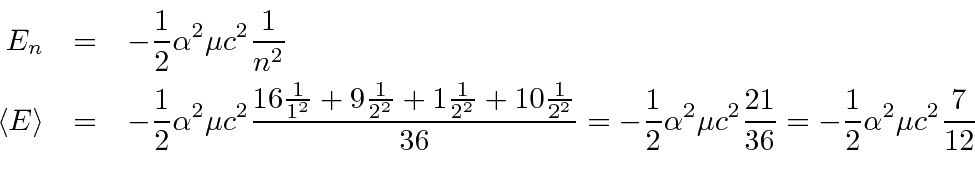
Similarly, we can just square probability amplitudes to compute the expectation value of
![]() .
The eigenvalues are
.
The eigenvalues are
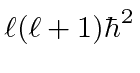 .
.
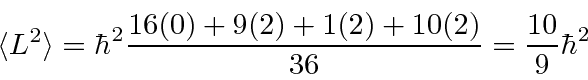
The Eigenvalues of
![]() are
are
![]() .
.
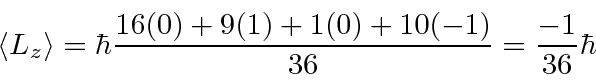
Computing the expectation value of
![]() is harder because the states are not eigenstates of
is harder because the states are not eigenstates of
![]() .
We must write
.
We must write
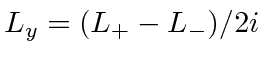 and compute.
and compute.
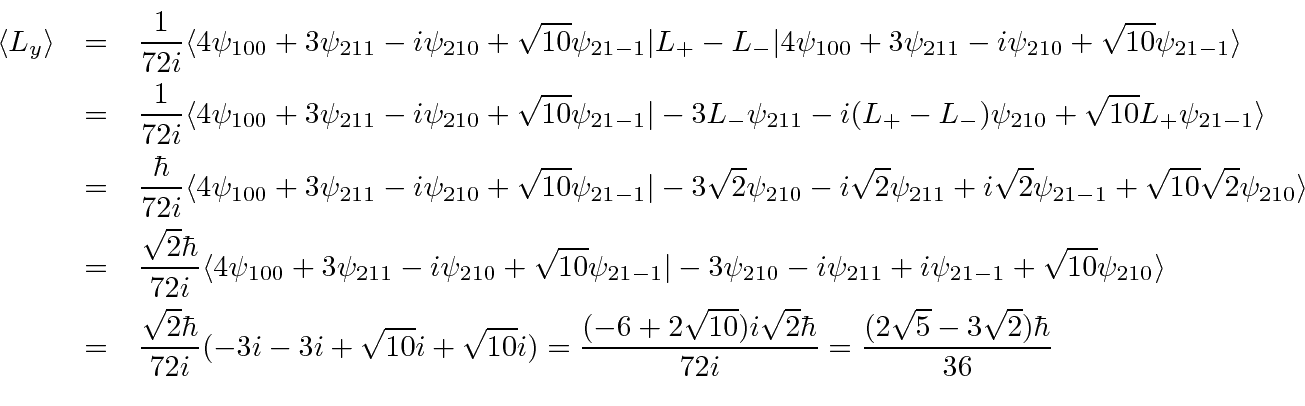
Jim Branson 2013-04-22