Next: The Potential Step Up: Piecewise Constant Potentials in Previous: Piecewise Constant Potentials in Contents
We have found the
general solution of the Schrödinger Equation in a region in which the potential is constant.
Assume the potential is equal to
![]() and the total energy is equal to
and the total energy is equal to
![]() .
Assume further that we are solving the time independent equation.
.
Assume further that we are solving the time independent equation.
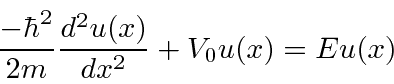
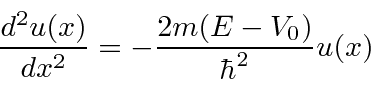
For
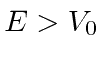 , the general solution is
, the general solution is
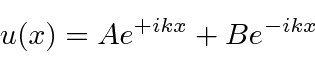
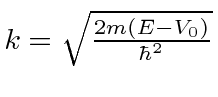 positive and real.
We could also use the linear combination of the above two solutions.
positive and real.
We could also use the linear combination of the above two solutions.
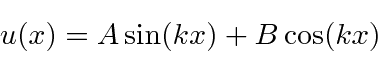
The solutions are also technically correct for
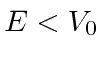 but
but
![]() becomes imaginary.
For simplicity, lets write the solutions in terms of
becomes imaginary.
For simplicity, lets write the solutions in terms of
 , which again is real and positive.
The general solution is
, which again is real and positive.
The general solution is
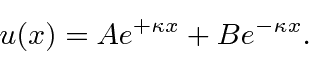
Jim Branson 2013-04-22