Next: Derivations and Computations Up: Eigenfunctions, Eigenvalues and Vector Previous: The Same Problem with Contents
We can also look at the eigenfunctions of the momentum operator.
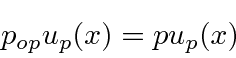
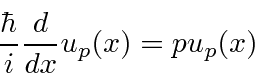
The eigenstates are
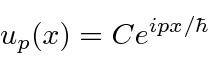
These solutions do not go to zero at infinity so they are not normalizable to one particle.
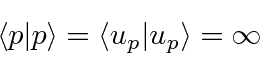
We will use a
different type of normalization for the momentum eigenstates
(and the position eigenstates).
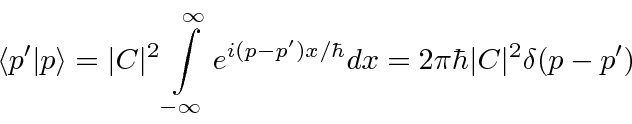
These are the momentum eigenstates
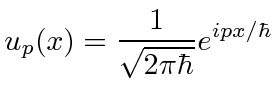 |
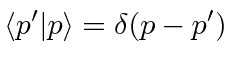 |
For a free particle Hamiltonian,
both momentum and parity commute with
![]() .
So we can make simultaneous eigenfunctions.
.
So we can make simultaneous eigenfunctions.
![\begin{eqnarray*}[H,p]=0 \\
{[H,P]=0} \\
\end{eqnarray*}](img1177.png)
![\begin{displaymath}\bgroup\color{black} [P,p]\neq 0 .\egroup\end{displaymath}](img1178.png)
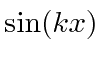 and
and
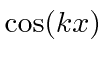 states which contain two momenta but are
eigenstates of
states which contain two momenta but are
eigenstates of
Jim Branson 2013-04-22